Đếm số lượng số nguyên dương không vượt quá N mà chia hết cho A hoặc B. Ràng buộc: 0 < A, B ≤ N ≤ 2.~10^9~

Dữ liệu vào: Gồm 1 dòng duy nhất chứa 3 số nguyên dương N, A và B.

Dữ liệu ra: Gồm 1 dòng duy nhất chứa số nguyên là kết quả bài toán.

Ví dụ:

Input:

6 2 3

Output:

4

Đếm số lượng số nguyên dương không vượt quá N mà chia hết cho cả A và B

Ràng buộc: 0 < A, B ≤ N ≤ ~9.10^{15}~

Dữ liệu vào:

• Gồm 1 dòng duy nhất chứa 3 số nguyên dương N, A và B.

Dữ liệu ra:

• Gồm 1 dòng duy nhất chứa số nguyên là kết quả bài toán.

Ví dụ:

Input:

12 2 3

Output:

2

Trên đường đi học về An đi qua một con phố có N ngôi nhà được đánh số từ 1 đến N. Những ngôi nhà bên trái của dãy phố được đánh số lẻ, ở bên phải được đánh số chẵn. An vừa đi vừa nhìn sang bên trái và sang phải rồi tính nhẩm tổng các số nhà ở hai bên con phố.

Yêu cầu: Em hãy giúp An tính tổng các số nhà ở dãy bên phải và bên trái con phố?

Input:

• Nhập vào số nguyên dương N.

Output:

• Dòng 1: Chứa số nguyên dương K là tổng các số nhà được đánh số lẻ.
• Dòng 2. Chứa số nguyên M là tổng các số nhà được đánh số chẵn.

Example:

Input:

10

Output:

25
30

Constraint:

~0 < N \le 10^9~

Mùa hè thời tiết nắng nóng dẫn đến mức tiêu thụ điện tăng cao, cùng với đó là tăng chi phí tiền điện phải trả. Là một học sinh đã học lập trình, em hãy giúp bố mẹ tính tiền điện phải trả hàng tháng qua đó có giải pháp để tiết kiệm điện. Giả sử tiền điện được tính giá bậc thang theo các mức sau:

Mức 1: Giá 1700Vnđ/KWh, tính cho 100KW đầu tiên

Mức 2: Giá 1900Vnđ/KWh tính cho 50KW tiếp theo(từ 101KW đến 150KW)

Mức 3: Giá 2100Vnđ/KWh tính cho 50KW tiếp theo (từ 151KW đến 200KW)

Mức 4: Giá 2500Vnđ/KWh tính từ 201KW trở lên.

Yêu cầu: Tính số tiền điện phải trả khi biết chỉ số công tơ điện của tháng này và tháng trước liền kề.

Input:

• Nhập vào 2 số nguyên dương M,N theo thứ tự là chỉ số công tơ điện của tháng này và tháng trước liền kề, hai số cách nhau 1 dấu cách.

Output:

• Ghi K là số tiền điện phải trả của tháng này.

Example:

Input1:

190 100

Output1:

153000

Input2:

370 200

Output2:

307000

Constraint:

~N < M < 2.10^5~

Cho số nguyên dương ~N~. Hãy viết chương trình tìm ước số lớn nhất của ~N~ mà khác 1 và chính nó.

Input:

• Dòng thứ nhất chứa số ~T~(~1≤T≤70~) thể hiện số lượng test case.
• T dòng tiếp theo, mỗi dòng chứa số nguyên ~N~. (~1≤N≤10^{12}~).

Output:

• Ứng với mỗi testcase, in ra đáp án cần tìm (nếu không có đáp án thì in ra ~-1~).

Example

Input:

5
1
2
4
6
8

Output:

-1
-1
2
3
4

Số nguyên ~K~ được gọi là ước của ~N~ khi ~N~ chia hết cho K. Ví dụ: ~N=6~, ~N~ có 4 ước nguyên dương là: 1,2,3,6.

Cho số nguyên dương ~N~ và dãy gồm ~N~ số nguyên ~A_1, A_2, A_3,…, A_N~.

Yêu cầu: Hãy tìm và in ra số có nhiều ước nguyên dương nhất. Nếu có nhiều số cùng có số lượng ước lớn nhất và bằng nhau thì in ra số đầu tiên tìm thấy trong dãy đã cho.

Input:

• Dòng 1. Ghi số nguyên dương ~N~
• Dòng 2. Ghi ~N~ số nguyên ~A_1, A_2, A_3,…, A_N~.

Output:

• In ra số nguyên có nhiều ước nguyên dương nhất trong dãy đã cho.

Example:

Input:

5
1 2 12 16 17

Output:

12
Giải thích: trong 5 số đã cho, số 12 có 6 ước và nhiều nhất.

Constraints:

~1 < N,A_i \le 10^6~

Trong buổi học Toán tiếp theo, Thầy lại cho ôn tập về số học, trong đó có các khái niệm: ước số, số chính phương, số nguyên tố, … và cho bài tập về nhà cho cả lớp tự luyện tập.

Khái niệm:

• Số chính phương là số tự nhiên có căn bậc hai là một số tự nhiên, hay nói cách khác, số chính phương bằng bình phương (lũy thừa bậc 2) của một số nguyên.
• Số nguyên ~𝑏~ (~𝑏 ≠ 0~) gọi là ước số của số nguyên ~𝑎~, nếu ~𝑎~ chia hết cho ~𝑏~.
• Số nguyên tố là số tự nhiên chỉ có 2 ước số, gồm 1 và chính nó.

Yêu cầu: Bài tập về nhà Thầy cho dãy số ~A~ có ~𝑛~ phần tử ~𝑎_1, 𝑎_2, … , 𝑎_𝑛~ và hỏi có bao nhiêu số có đúng 3 ước số dương trong dãy số ~A~.

Dữ liệu vào:

• Dòng 1: Chứa duy nhất số nguyên dương ~𝑛~ (~1 ≤ 𝑛 ≤ 10^4~).
• Dòng 2: Gồm ~n~ số nguyên dương ~𝑎_𝑖~ (~0 < 𝑎_𝑖 ≤ 10^9:∀1 ≤ 𝑖 ≤ 𝑛~), giữa các số cách nhau bởi một dấu cách.

Kết quả:

• Ghi duy nhất số nguyên dương là số lượng số có đúng 3 ước số dương. Nếu không có số nào thỏa mãn thì ghi 0.

Ví dụ:

Input

4
3 9 8 81

Output

1

Ràng buộc: ▪ ~1 ≤ n ≤ 10^4; 0 < a_i ≤ 10^9:∀1 ≤ i ≤ n~

Tính tổng và số lượng các số hạng của dãy số sau: A= 1 + 2 + 3 + 4 +…..+ N

Input:

• Nhập vào một số nguyên dương N

Output:

• Ghi ra 2 số nguyên lần lượt là số lượt số hạng và tổng các số hạng của dãy số.

Example:

Input:

5

Output:

5 15

Constraints:

~0 < N \le 10^9~

Tính tổng và số lượng các số hạng của dãy số sau: A= 1 + 4 + 7 + 10 +…..+ N

Input:

• Nhập vào một số nguyên dương N

Output:

• Ghi ra 2 số nguyên lần lượt là số lượt số hạng và tổng các số hạng của dãy số.

Example:

Input:

7

Output:

3 12

Constraints:

~0 < N \le 10^9~

Tính tổng dãy số: ~1 - 2 + 3 - 4 + ..... N~.

Input

• Dòng đầu tiên và duy nhất chứa 1 số nguyên N ~(N \le 10^9)~

Output

• In ra một số nguyên là đáp số của tổng trên.

Example

Input

4

Output

-2

Cho dãy số ~𝑇_1, 𝑇_2, 𝑇_3 … , 𝑇_𝑛~ Với số hạng tổng quát ~𝑇_𝑘 = (𝑘 + 1)^2 - 𝑘^2~ (~𝑘~ là số nguyên và ~1 ≤ 𝑘 ≤ 𝑛~).

Yêu cầu: tính giá trị ~𝑆 = 𝑇1 + 𝑇2 + 𝑇3 + ⋯ + 𝑇_𝑛~

Dữ liệu vào:

• Một số nguyên dương (~𝑛 ≤ 10^9~).

Dữ liệu ra:

• Một số nguyên là giá trị ~𝑆~ tính được.

Ví dụ

Input

2

Output

8

Tính tổng và số lượng các số hạng của dãy số sau: A= 2 + 7 + 12 + 17 + …..+ N

Input:

• Nhập vào một số nguyên dương N.

Output:

• Ghi ra tổng các số hạng của dãy số.

Example:

Input:

12

Output:

21

Constraints:

~0 < N \le 10^9~

Tính tổng dãy số: ~1 - 3 + 5 - 7 + 9 - ..... + N~.

Input

• Dòng đầu tiên và duy nhất chứa 1 số tự nhiên lẻ N ~(N \le 10^9)~

Output

• In ra một số nguyên là đáp số của tổng trên.

Example

Input

9

Output

5

Cho tam giác ABC có tọa độ 3 đỉnh là A(xa,ya),B(xb,yb),C(xc,yc) như hình.

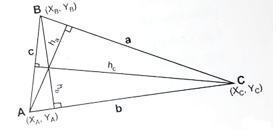
Ví dụ:

Input

-9 11 -3 5 -3 -4

Output

27.000
6.000 3.343 6.364

Nhập vào từ bàn phím 2 số nguyên dương ~x,y~ (~x,y \le 60000~). Hãy tìm và in ra màn hình số nguyên dương ~z~ sao cho tam giác có độ dài 3 cạnh là 3 số ~x,y,z~ là tam giác cân có diện tích lớn nhất.

Input

• Hai số nguyên dương

Output

• In ra một số nguyên dương

Example

Input

5
7

Output

7

Cho phân số a/b (a nguyên; b nguyên; ~0 \le a \le 2.10^9; 1 \le b \le 2.10^9~).

Yêu cầu: Rút gọn phân số để phân số trở thành phân số tối giản.

Input:

• Nhập vào 2 số a, b cách nhau ít nhất 1 ký tự trắng.

Output:

• In kết quả phân số a/b sau khi rút gọn

Example:

Input:

6 9

Output:

2/3

Viết chương trình cho phép cộng 2 phân số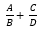

Dữ liệu vào

• Dòng 1: 2 số nguyên ~A~, ~B~.
• Dòng 2: 2 số nguyên ~C~, ~D~.

Ràng buộc: ~0 \le A,B,C,D \le 10^9~

Dữ liệu ra

• Dòng 1: Ghi kết quả của phép cộng 2 phân số sau khi đưa về phân số tối giản.

  Ví dụ

Input1

3 5
7 8

Output1

59/40

Input2

35 6
7 6

Output2

7

Input3

-35 6
18 6

Output3

-17/6

Viết chương trình cho phép trừ 2 phân số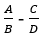

Dữ liệu vào

• Dòng 1: 2 số nguyên dương A, B.
• Dòng 2: 2 số nguyên dương C, D.

Ràng buộc: ~0 \le A,B,C,D \le 10^9~

Dữ liệu ra

• Dòng 1: Ghi kết quả của phép trừ 2 phân số sau khi đưa về phân số tối giản.

  Ví dụ

Input

3 5
6 9

Output

-1/15

Input

35 6
11 6

Output

4

Có 𝑚 ông táo và 𝑛 bà táo được Ngọc Hoàng phân công nhiệm vụ trong năm mới. Đầu tiên Ngọc Hoàng chọn 𝑘 táo (ông hoặc bà) làm những nhiệm vụ đặc biệt tại các Bộ/Ngành, sau đó Ngọc Hoàng sẽ chọn ra các nhóm, mỗi nhóm gồm đúng 2 ông táo và 1 bà táo để phân công xuống các gia đình dưới hạ giới.

Yêu cầu: Hãy giúp Ngọc Hoàng xác định số nhóm nhiều nhất để phân công xuống các gia đình dưới hạ giới.

Input:

• Nhập vào 3 số nguyên dương m,n,k

Output:

• Ghi 1 số nguyên duy nhất là số nhóm tối đa để phân công xuống hạ giới.
• Ví dụ: có 𝑚 = 12 ông táo và 𝑛 = 7 bà táo, có 𝑘 = 5 táo phải làm nhiệm vụ đặc biệt. Ngọc Hoàng có thể chọn tối đa 4 nhóm phân xuống các gia đình (8 ông táo và 4 bà táo). Trong 7 táo còn lại (4 ông và 3 bà) có 5 táo làm nhiệm vụ đặc biệt, còn 2 táo không được phân việc.

Example:

Input:

12  7  5

Output:

4

Constraints:

~0 < m,n,k \le 10^9~

Tèo là một người rất yêu các dãy số. Một hôm, Tèo không có việc gì làm nên chán nản. Đột nhiên, Tèo nổi hứng nghĩ ra một công việc kì lạ: đó là viết các số lẻ trong khoảng 1 đến ~N~ rồi các số chẵn trong khoảng 1 đến ~N~. Sau đó Tèo chọn ra số ~K~ đầu tiên. Tèo không biết số thứ ~K~ có giá trị là bao nhiêu. Em hãy giúp Tèo nhé.

Dữ liệu vào:

• Gồm 1 dòng duy nhất chứa hai số nguyên dương ~N~ và ~K~.

Dữ liệu ra:

• Gồm 1 dòng duy nhất chứa một số ~t~ là kết quả bài toán.

Ví dụ:

Input 1

10 3

Output 1

5

Input2

7 7

Output2

6

Ràng buộc

• ~1≤ K ≤ N ≤ 10^{12}~

Dãy fibonaci là dãy vô hạn các số tự nhiên bắt đầu bằng 2 phần tử 1, 1. Các phần tử sau đó được thiết lập theo quy tắc mỗi phần tử luôn bằng tổng 2 phần tử liền trước nó. Ví dụ: n=3, số fibonaci thứ 3 là: 1+1=2.

Yêu cầu: Hãy tìm số fibonaci thứ ~n~.

Input:

• Nhập vào một số nguyên dương ~n~.

Output:

• In ra số nguyên dương thứ ~n~ sau khi đã mod cho ~10^9+7~.

Example:

Input:

8

Output:

21

Constraints:

~0 < n \le 10^9~

Vừa gà vừa chó

Bó lại cho tròn

Tổng n con

Và k chân chẵn

Yêu cầu: Tính số gà, số chó biết n, k là 2 số nguyên dương cho trước.

Input:

• Nhập vào 2 số nguyên dương n, k.

Output:

• Ghi 2 số nguyên x,y tương ứng là số gà số chó tìm được. Nếu không tìm được x,y thỏa mãn thì ghi -1.

Example:

Input:

36 100

Output:

22 14

Constraints:

~0 < n < k < 2*10^9~

Htmaths2512 sống ở Sao Hoả, cậu có thể thọ tỷ Nam Sơn. Htmaths2512 có một người Bố thật tuyệt vời, cậu muốn lớn thật nhanh để có thể làm được những việc như bố.

Em hãy lập trình nhập vào 2 số nguyên dương a, b lần lượt là số tuổi của bố và Htmaths2512 hiện tại, tính và thông báo ra màn hình bao nhiêu năm nữa tuổi bố sẽ gấp đôi tuổi Htmaths2512.

Input:

• Ghi 2 số nguyên dương a, b.

Output:

• In ra số nguyên dương N là số năm để tuổi bố gấp đôi tuổi Ht_maths2512.

Input:

30 5

Input:

20

constraint:

%: ~1 \le a,b \le 10^{18}~

Hiệp sỹ Petrein đến làm khách ở Chúa tể Bóng đêm đã được vài tuần, được nghe về các kỳ tích hiển hách của vị Chúa tể trong những năm gần đây và hiểu rằng đã lâu lắm mình chưa lập một kỳ tích nào cả. Cùng nhau cân nhắc kỹ lưỡng bên chén trà hai người thống nhất là Petrein phải đi giết con Rồng lửa đang tác oai tác quái phía tây của vương quốc. Nhưng có hiệp sỹ nào lên đường mà không có giáp phục, giáo và khiên! Petrein hiện đang có 2 cái khiên hình tam giác, nhưng ông cho rằng như thế là chưa đủ. Khiên phải càng to càng tốt và ông quyết định giao cho thợ rèn làm khiên mới từ 2 khiên hiện có. Người thợ rèn của hoàng cung đề nghị hàn mép của hai khiên nối chúng thành một khiên duy nhất. Petrein nhận thấy dù có hàn cách nào diện tích khiên mới cũng không đổi, vì vậy ông đề nghị hàn sao cho chu vi của khiên mới là nhỏ nhất để không phải tốn nhiều vàng làm đường viền cho khung. Cái khiên phải mang biểu tượng của gia tộc!

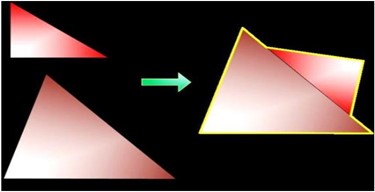
Yêu cầu: Cho 6 số nguyên 𝑎1 , 𝑏1 , 𝑐1 và 𝑎2 , 𝑏2 , 𝑐2 là độ dài các cạnh của 2 khiên. Hãy xác định chu vi nhỏ nhất có thể nhận được.

Input:

• Dòng 1: Chứa 3 số nguyên 𝑎1 , 𝑏1 , 𝑐1 .
• Dòng 2: Chứa 3 số nguyên 𝑎2 , 𝑏2 , 𝑐2 . ~(𝑎1 , 𝑏1 , 𝑐1 , 𝑎2 , 𝑏2 , 𝑐2 ≤ 10^6)~

Output:

• Dòng 1: Ghi 1 số nguyên là chu vi nhỏ nhất có thể nhận được sau khi hàn 2 tấm khiên.

Example:

Input:

3 4 5
6 7 8

Output:

23

Thầy Sơn phát kẹo cho N bạn học sinh; mỗi bạn sẽ được phát M viên kẹo. Siêu thị bán kẹo theo gói đóng sẵn, mỗi gói gồm K viên kẹo.

Yêu cầu: Cho 3 số N, M, K hãy tính số gói kẹo ít nhất thầy Sơn cần mua để phát đủ kẹo cho các bạn ~1 \le N,M,K \le 10^{12}~

Input:

• Dòng đầu tiên lần lượt là ba số nguyên dương N, M, K;

Output:

• In ra một số nguyên duy nhất là số gói kẹo cần mua.

  Example:

Input:

5 4 10 

Output:

2

Giải thích: Mua 2 gói kẹo sẽ được 20 viên kẹo, chia cho 5 bạn thì mỗi bạn được chính xác 4 viên.

Có ba đống đá. Đống thứ nhất chứa ~𝑎~ viên đá, đống thứ hai chứa ~𝑏~ viên đá và đống thứ ba chứa ~𝑐~ viên đá. Bạn phải chọn ra một trong số các đống đá đó và chia đá từ đống đó vào hai đống kia. Cụ thể, nếu đống đá ban đầu bạn chọn chứa ~𝑠~ viên, bạn hãy di chuyển ~𝑘~(~0 \le 𝑘 \le 𝑠~) viên đá từ đống đã chọn sang một trong hai đống còn lại và ~𝑠 - 𝑘~ viên đá vào đống còn lại.

Yêu cầu: Hãy cho biết có tồn tại hay không một cách chia để thu được hai đống đá chứa ~𝑥~ và ~𝑦~ viên đá.

Input:

• Dòng 1: 5 số nguyên 𝑎, 𝑏, 𝑐, 𝑥, 𝑦.(~1 \le 𝑎, 𝑏, 𝑐, 𝑥, 𝑦 \le 10^9~).

Output

• Dòng 1: Nếu có cách chia thì ghi "YES", nếu không có cách chia thì ghi "NO".

Example

Input:

2 4 2 6 2

Output:

YES

Input:

3 2 5 6 5

Output:

NO

Hai bạn An và Bách cùng học một trường nhưng ở 2 lớp khác nhau. An cứ a ngày lại trực nhật một lần; Bách cứ b ngày lại trực nhật một lần. Lần đầu cả hai người cùng trực nhật vào cùng một ngày. Hỏi sau ít nhất bao nhiêu ngày thì hai bạn lại cùng trực nhật cùng ngày? Lúc đó mỗi bạn đã trực nhật được bao nhiêu lần?

Dữ liệu vào:

• 2 số nguyên a,b.(~1 \le a,b \le 200000~)

Dữ liệu ra:

• In ra theo ví dụ sau

Ví dụ:

Input

10
12

Output

60
An: 6
Bach: 5

Cho một khóa số, có ~n~ vòng số (~3 ≤ n ≤ 10~), mỗi vòng có 10 chữ số từ 0 đến 9 được xếp thứ tự như ví dụ bên dưới. Trên ổ khóa có 01 vị trí được đánh dấu mũi tên cho biết ~n~ chữ số hiện hành của ổ khóa, muốn mở khóa chúng ta xoay các vòng lên hay xuống từng nấc để thay đổi số hiện hành sao cho trùng với mật khẩu đã cho trước, đúng thứ tự từ trái qua phải thì khóa sẽ mở. Quy ước vòng đầu tiên bên trái là vòng 1,… vòng cuối cùng bên phải là vòng ~n~

Hình trên là khoá số có 5 vòng; 5 chữ số hiện hành là 00000. Quy ước: Giả sử 1 vòng của ổ khóa có số hiện hành là số 0: nếu xoay lên 1 nấc thì số hiện hành là số 1, ngược lại nếu xoay xuống 1 nấc thì số hiện hành là số 9.

Yêu cầu: Nhập số vòng ~n~ của ổ khóa, ~n~ chữ số hiện hành trên ổ khóa và mật khẩu ~n~ chữ số từ ~0~ đến ~9~. Cho biết tổng số nấc xoay ít nhất của ~n~ vòng để mở được ổ khóa.

Dữ liệu vào:

• Dòng 1: số nguyên ~n~ – số vòng
• Dòng 2: ~n~ chữ số hiện hành
• Dòng 3: mật khẩu gồm ~n~ chữ số.

Dữ liệu ra:

• Xuất kết quả ra màn hình 1 số duy nhất là tổng số nấc xoay ít nhất của ~n~ vòng để mở được ổ khóa.

Ví dụ:

Input:

5 
00000
63082

Output:

11

Mặt của đồng hồ kim là một hình tròn được chia thành 60 vạch và được đánh số từ 0 đến 59. Hiện tại, kim phút chỉ vào vạch có chỉ số là ~𝑚~ (~0 ≤ 𝑚 ≤ 59~) và cứ sau một phút, kim phút dịch chuyển sang vạch bên cạnh theo chiều quay của kim đồng hồ.

Yêu cầu: Hãy cho biết sau ~𝑛~ phút thì kim phút chỉ vào vạch số mấy?

Dữ liệu vào:

• Gồm hai số nguyên ~𝑚~ và ~𝑛~ (~1≤𝑛≤10^{18}~).

Kết quả:

• Ghi một số nguyên là kết quả bài toán.

Ví dụ:

Input

5 19

Output

24

Cho 3 số ~a, b, h~ là 3 kích thước của một hình hộp chữ nhật (~1 ≤ a, b, h ≤ 32767~).

Yêu cầu: Tính diện tích toàn phần của hình hộp chữ nhật.

Dữ liệu vào:

• Dòng 1: Ghi lần lượt 3 số nguyên dương a,b,h cách nhau ít nhất 1 ký tự trắng.

Dữ liệu ra:

• Dòng 1: Ghi 1 số nguyên dương duy nhất là diện tích toàn phần của hình hộp chữ nhật.

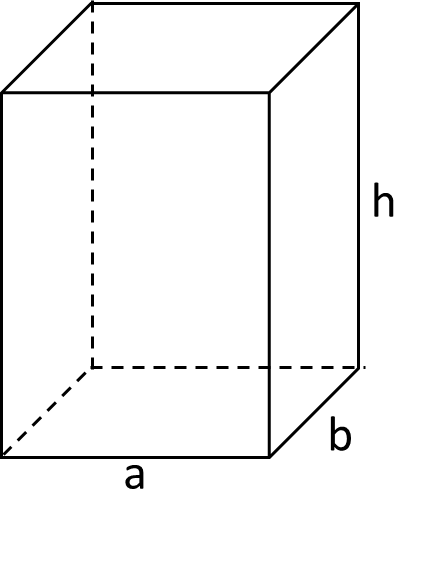
Ví dụ:

Input

1  1  2

Output

10

Cho số ~π= 3.1415926535897~

Lập trình tính diện tích hình vành khuyên có bán kính ngoài là ~r_1~ và bán kính trong là ~r_2~ (xem hình)

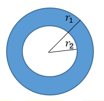
Dữ liệu vào:

• Hai số thực ~r_1,r_2~ (~0<r_1,r_2≤100~)</li>

Kết quả:

• Diện tích hình vành khuyên tìm được với độ chính xác 4 chữ số thập phân

Ví dụ:

Input

1.63 1.55

Output

0.7992

Cho số tự nhiên ~n~. Hãy viết chương trình tính ~S = 1^3 + 2^3 + 3^3 + … + n^3~.

Dữ liệu vào:

• Gồm một dòng duy nhất chứa số nguyên ~n~ (~1 \le n \le 10^9~).

Dữ liệu ra:

• Ghi một giá trị duy nhất làị số dư của phép chia ~S~ cho ~10^9+7~

Ví dụ:

Input1

3

Output1

36

Input2

4

Output2

100

Ràng buộc:

• 70% test ứng với giới hạn ~1 \le n \le 10^4~
• 30% test ứng với các trường hợp còn lại