CONTEST 21: ÔN TẬP CHUYÊN ĐỀ: TIỀN TỐ (PREFIX)
Đếm số âm
Nộp bàiPoint: 8
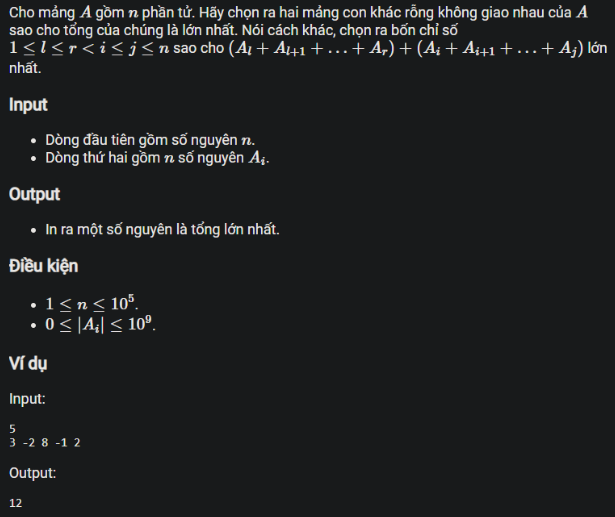
Cho dãy ~𝐴~ gồm ~𝑛~ số nguyên dương ~𝑎_1, 𝑎_2, . . , 𝑎_𝑛~. Cho ~𝑞~ truy vấn có dạng ~𝑙~, ~𝑟~
Yêu cầu: Với mỗi truy vấn ~𝑙~, ~𝑟~ hãy đếm số lượng các số có giá trị âm từ phần tử thứ ~l~ đến phần tử thứ ~r~ của dãy số ~A~.
Dữ liệu vào:
- Dòng thứ nhất ghi 2 số nguyên dương ~𝑛~ và ~𝑞~ (~1 ≤ 𝑛,𝑞 ≤ 10^6~)
- Dòng thứ hai ghi ~𝑛~ số nguyên ~𝑎_1, 𝑎_2, … , 𝑎_𝑛~ các số có giá trị tuyệt đối không vượt quá ~10^6~
- ~𝑞~ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương ~𝑙~, ~𝑟~ (~1 ≤ 𝑙 ≤ 𝑟 ≤ 𝑛~)
Dữ liệu ra:
- ~𝑞~ dòng mỗi dòng ghi một số nguyên dương là kết quả tìm được của mỗi truy vấn.
Ví dụ
Input
9 3
1 -3 8 9 -7 -9 9 7 -1
1 6
2 7
6 9
Output
3
3
2
Đếm số dương
Nộp bàiPoint: 8
Cho dãy ~𝐴~ gồm ~𝑛~ số nguyên dương ~𝑎_1, 𝑎_2, . . , 𝑎_𝑛~. Cho ~𝑞~ truy vấn có dạng ~𝑙~, ~𝑟~
Yêu cầu: Với mỗi truy vấn ~𝑙~, ~𝑟~ hãy đếm số lượng các số có giá trị dương từ phần tử thứ ~l~ đến phần tử thứ ~r~ của dãy số ~A~.
Dữ liệu vào:
- Dòng thứ nhất ghi 2 số nguyên dương ~𝑛~ và ~𝑞~ (~1 ≤ 𝑛,𝑞 ≤ 2.10^6~)
- Dòng thứ hai ghi ~𝑛~ số nguyên ~𝑎_1, 𝑎_2, … , 𝑎_𝑛~ các số có giá trị tuyệt đối không vượt quá ~10^6~
- ~𝑞~ dòng tiếp theo, mỗi dòng chứa hai số nguyên dương ~𝑙~, ~𝑟~ (~1 ≤ 𝑙 ≤ 𝑟 ≤ 𝑛~)
Dữ liệu ra:
- ~𝑞~ dòng mỗi dòng ghi một số nguyên dương là kết quả tìm được của mỗi truy vấn.
Ví dụ
Input
9 3
1 -3 8 9 -7 -9 9 7 -1
1 6
2 7
6 9
Output
3
3
2
Đếm số âm (Premium)
Nộp bàiPoint: 8
Trên một màn hình lớn, người ta lần lượt cho xuất hiện các số của một dãy gồm 𝑛 số nguyên ~𝑎_1,𝑎_2,…,𝑎_𝑛~ và cứ lặp đi lặp lại như thế (nghĩa là sau khi ~𝑎_𝑖~ xuất hiện vài giây đến lượt ~𝑎_𝑖+1~ xuất hiện, số xuất hiện sau ~𝑎_𝑛~ là ~𝑎_1~).
Yêu cầu: Hãy đếm số lượng số âm của 𝑘 số xuất hiện liên tiếp trên màn hình bắt đầu từ lần thứ xuất hiện thứ ~𝑚~.
Dữ liệu vào:
- Dòng đầu tiên gồm ba số nguyên ~𝑛~,~𝑘~,~𝑚~.
- Dòng 2: Ghi ~𝑛~ số nguyên ~𝑎_𝑖~.
Dữ liệu ra:
- Ghi số nguyên dương là số lượng số âm tìm được.
Ví dụ:
Input:
5 7 2
-56 56 -41 35 4
Output:
3
Giới hạn dữ liệu:
~𝑛<10^3~; ~𝑘<10^9~; ~𝑎_𝑖<10^6~
Trong bộ test có:
40% test có ~𝑚+𝑘≤𝑛~
40% test có ~𝑚+𝑘< 10^7~
Đếm số dương (Premium)
Nộp bàiPoint: 10
Trên một màn hình lớn, người ta lần lượt cho xuất hiện các số của một dãy gồm 𝑛 số nguyên ~𝑎_1,𝑎_2,…,𝑎_𝑛~ và cứ lặp đi lặp lại như thế (nghĩa là sau khi ~𝑎_𝑖~ xuất hiện vài giây đến lượt ~𝑎_𝑖+1~ xuất hiện, số xuất hiện sau ~𝑎_𝑛~ là ~𝑎_1~).
Yêu cầu: Hãy đếm số lượng số dương của 𝑘 số xuất hiện liên tiếp trên màn hình bắt đầu từ lần thứ xuất hiện thứ ~𝑚~.
Dữ liệu vào:
- Dòng đầu tiên gồm ba số nguyên ~𝑛~,~𝑘~,~𝑚~.
- Dòng 2. Chứa ~𝑛~ số nguyên ~𝑎_𝑖~.
Dữ liệu ra:
- Ghi số nguyên dương là số lượng số dương tìm được.
Ví dụ:
Input:
5 7 9
3 -5 7 -8 6
Output:
4
Giới hạn dữ liệu:
~𝑛<10^3~; ~𝑘<10^9~; ~𝑎_𝑖<10^6~
Trong bộ test có:
40% test có ~𝑚+𝑘≤𝑛~
40% test có ~𝑚+𝑘< 10^7~
Tổng dãy con liên tiếp
Nộp bàiPoint: 10
Cho một mảng a có ~N~ phần tử và ~Q~ truy vấn. Mỗi truy vấn sẽ cho 2 số ~x~ và ~y~, bạn sẽ phải cho biết tổng ~a[x] + a[x+1] + a[x+2] + ... + a[y]~ bằng bao nhiêu.
Input:
Được cho bởi tệp SUMARR.INP có cấu trúc như sau:
- Dòng đầu chứa số ~N~.
- Dòng thứ 2 chứa ~N~ số, là miêu tả mảng ~a~.
- Dòng thứ 3 chứa số ~Q~.
- ~Q~ dòng sau, mỗi dòng chứa 2 số ~x~ và ~y~.
Output:
- Được cho bởi tệp SUMARR.OUT gồm ~Q~ dòng, mỗi dòng chứa số nguyên là tổng các phần tử từ ~x~ đến ~y~ tương ứng.
Example:
Input:
6
1 2 3 2 1 2
3
1 3
2 4
1 6
Output:
6
7
11
Constraints:
~N \le 10^5 ; a[i] \le 10^9 ; Q \le 10^5; 1 \le x \le y \le N~
Tổng Dãy Con
Nộp bàiPoint: 10
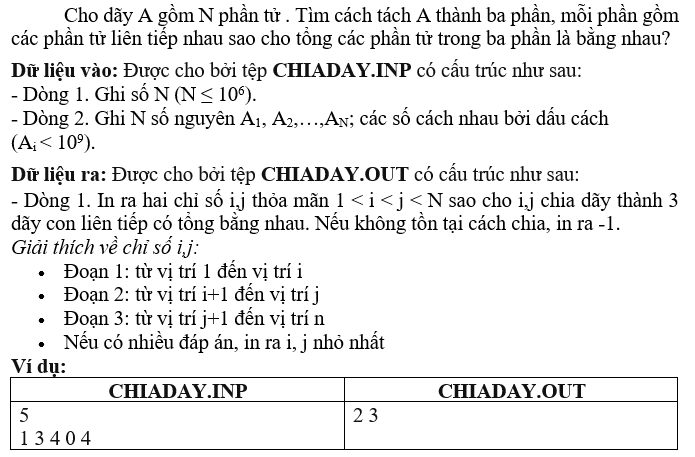
Cho dãy ~A~ gồm ~N~ phần tử.
Một dãy ~a~ là dãy con của dãy ~b~ khi và chỉ khi ta xóa đi một số phần tử trong dãy ~b~ sẽ thu về dãy ~a~.
Cụ thể với ~a = [1, 2, 3]~ sẽ là dãy con của ~b = [1, 4, 5, 2, 10, 3]~. Và dãy ~a~ = [] (rỗng) cũng là một dãy con của ~b = [1, 4, 5, 2, 10, 3]~.
Yêu cầu: Với ~q~ truy vấn, mỗi truy vấn gồm 1 cặp số ~l~ và ~r~ ~(1 <= l <= r <= N)~. Hãy tìm dãy con của dãy ~A_l, A_{l + 1}, ..., A_{r - 1}, A_{r}~ có tổng lớn nhất và in ra tổng đó.
INPUT
- Dòng đầu chứa 2 số ~N~ và ~q~ ~(1 <= N, q, <= 10^5)~
- Dòng thứ 2 chứa dãy ~A~ gồm ~n~ phần tử ~(|A_i| <= 10^7)~
- ~q~ dòng tiếp theo, mỗi dòng gồm 1 cặp số ~l~ và ~r~
OUTPUT
- Với mỗi testcase, in ra yêu cầu của bài
SUBTASKS
- Subtask 1 (40%): ~q <= 10^4, n <= 10^2~
- Subtask 2 (60%): ~q <= 10^5, n <= 10^5~
SAMPLE
Input
7 2
1 -2 3 -4 5 -6 7
1 5
3 6
Output
9
8
Explanation
Dãy con có tổng lớn nhất từ:
1 -> 5: 1 + 0 + 3 + 0 + 5 = 9
3 -> 6: 3 + 0 + 5 + 0 = 8
Mật khẩu(HSG 9 Quảng Bình 2023 - 2024)
Nộp bàiPoint: 8
Mật khẩu là một xâu ký tự. Một mật khẩu được gọi là an toàn nếu thoả mãn các điều kiện sau:
- Có độ dài ít nhất bằng 8
- Chứa ít nhất một chữ cái in hoa ['A'..'Z']
- Chứa ít nhất một chữ cái in thường ['a'..'z']
- Chứa ít nhất một chữ số ['0'..'9']
Cho một xâu ký tự có độ dài không quá 1000 ký tự.
Yêu cầu: Hãy xác định có bao nhiêu đoạn con gồm các ký tự liên tiếp nhau trong xâu S có thể chọn làm mật khẩu an toàn.
Input:
Được cho bởi tệp MATKHAU.INP có cấu trúc như sau:
- Dòng 1: Ghi xâu ký tự S
Output
Ghi ra tệp MATKHAU.OUT theo cấu trúc:
- Dòng 1. Ghi số nguyên dương t là kết quả tìm được theo yêu cầu.
Example
Input
ABC123abc
Output
3
Input
ABC123
Output
0
Constrains:
- Có 50% số test ứng với độ dài xâu ~S \le 50~
- Có 30% số test ứng với độ dài xâu ~50 \le S \le 300~
- Có 20% số test ứng với độ dài xâu ~300 \le S \le 1000~
Cắt thành 2 dãy
Nộp bàiPoint: 8
Cho mảng a có n số nguyên, hãy kiểm tra xem có thể cắt a thành 2 dãy liên tiếp có tổng bằng nhau hay không. Nếu có thể cắt thành hai dãy liên tiếp bằng nhau thì ghi như sau:
Input:
- Dòng 1: ghi số nguyên dương N
- Dòng 2: ghi N số nguyên
Output:
Nếu có thể cắt thành hai dãy liên tiếp bằng nhau thì ghi như sau:
- Dòng 1: ghi số 1
- Dòng 2: ghi các số của dãy 1, mỗi số ngăn cách nhau bởi ký tự trắng.
- Dòng 3. ghi các số của dãy 2, mỗi số ngăn cách nhau bởi ký tự trắng.
Nếu không thể cắt thành hai dãy liên tiếp bằng nhau thì ghi duy nhất số 0
Example:
Input:
5
88 99 100 13 300
Output:
1
88 99 100 13
300
Constraint:
~1 \le n \le 10000~; ~0 \le A_i \le 32000~;
Vòng tròn số
Nộp bàiPoint: 10
Cho một dãy gồm ~N~ số nguyên đánh số từ 1 đến N (~A_1, A_2,…, A_N; |a_i| ≤ 10^9~) và được sắp xếp thành một vòng tròn theo chiều kim đồng hồ.
Yêu cầu: Hãy tìm tổng lớn nhất ~K~ số liên tiếp trong vòng tròn trên.
Dữ liệu vào:
- Dòng 1. Ghi 2 số nguyên dương ~N, K~ (~0 < K < N ≤ 10^5~) cách nhau một dấu cách.
- Dòng 2. Chứa ~N~ số nguyên là các phần tử ~A_i~ của dãy, mỗi số có giá trị tuyệt đối không vượt quá ~10^6~, giữa các số cách nhau một dấu cách.
Dữ liệu ra:
- Dòng 1: Ghi số nguyên duy nhất là tổng lớn nhất của ~K~ số liên tiếp nhau tìm được trong vòng tròn số.
Ví dụ
Input
5 3
10 2 3 5 7
Output
22
Ràng buộc:
- 50% số test: ~0 ≤ K< N ≤ 10^4~ ;
- 50% số test: ~10^4 < K < N ≤ 10^5~ ;
Tổng hình chữ nhật
Nộp bàiPoint: 10
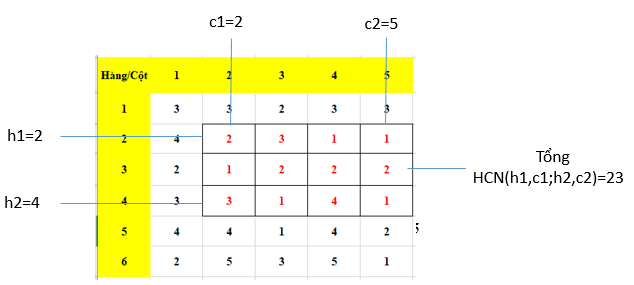
Cho một bảng gồm N hàng, M cột. Các hàng của bảng được đánh số từ 1 đến N từ trên xuống dưới, các cột của bảng được đánh số từ 1 đến M từ trái qua phải. Ô nằm trên giao của hàng i và cột j được gọi là ô (i, j) và trên đó chứa một số nguyên dương là A[i, j] (~1 ≤ i, j ≤ N~)
Yêu cầu: Ứng với mỗi bộ (~h1,c1~) và (~h2,c2~) cho trước hãy tính và in ra tổng tất cả các ô nằm trên hình chữ nhật được tạo bởi giao giữa hàng ~h1~, cột ~c1~; hàng ~h2~, cột ~c2~.
Dữ liệu vào:
Cho trong file tonghcn.inp có cấu trúc như sau:
- Dòng 1: Ghi hai số nguyên dương ~N~, ~M~ (~1 ≤ N ≤ M ≤ 10^3~ ).
- Dòng thứ i trong N dòng tiếp theo: Ghi ~M~ số nguyên dương, số thứ j là ~A[i, j]~ (~A[i, j] ≤ 10^3~).
- Dòng thứ N+2: Ghi số nguyên dương T là số lượng bộ test cần tìm (~T ≤ 10^3~.
- T dòng tiếp theo mỗi dòng ghi 4 số nguyên dương ~h_1, h_2, c_1, c_2~.
Dữ liệu ra:
Ghi ra file tonghcn.out với cấu trúc như sau:
- Gồm T dòng, mỗi dòng ghi tổng tìm được ứng với T test đã cho.
Ví dụ:
Input
3 4
1 2 3 4
3 2 1 2
2 3 1 3
2
1 3 2 4
1 2 3 4
Output
21
10
Tính tổng( Đề thi HSG THCS tỉnh Ninh Bình năm học 2021-2022)
Nộp bàiPoint: 10
Trên một màn hình lớn, người ta lần lượt cho xuất hiện các số của một dãy gồm 𝑛 số nguyên không âm ~𝑎_1,𝑎_2,…,𝑎_𝑛~ và cứ lặp đi lặp lại như thế (nghĩa là sau khi ~𝑎_𝑖~ xuất hiện vài giây đến lượt ~𝑎_𝑖+1~ xuất hiện, số xuất hiện sau ~𝑎_𝑛~ là ~𝑎_1~).
Yêu cầu: Hãy tính tổng của 𝑘 số xuất hiện liên tiếp trên màn hình bắt đầu từ lần thứ xuất hiện thứ ~𝑚~.
Dữ liệu vào:
- Dòng đầu tiên gồm ba số nguyên ~𝑛~,~𝑘~,~𝑚~.
- Trong ~𝑛~ dòng sau, dòng thứ ~𝑖~ chứa số ~𝑎_𝑖~.
Dữ liệu ra:
- Ghi giá trị tổng tìm được.
Ví dụ:
Input:
3 7 5
2
3
6
Output:
25
Giới hạn dữ liệu:
~𝑛<10^3~; ~𝑘<10^9~; ~𝑎_𝑖<10^6~
Trong bộ test có:
40% test có ~𝑚+𝑘≤𝑛~
40% test có ~𝑚+𝑘< 10^6~
Chia đoạn con có tổng bằng nhau
Nộp bàiPoint: 10
Cho mảng A có N số nguyên, hãy chia A thành nhiều đoạn con liên tiếp nhất có thể sao cho tổng các phần tử trên mỗi đoạn này đều bằng nhau.
Input:
- Dòng 1. Ghi số nguyên dương N
- Dòng 2. Ghi N số nguyên ~A_1, A_2….A_N~
Output:
- Dòng 1. Ghi số nguyên dương K là kết quả bài toán.
Example:
Input:
6
1 2 3 3 2 1
Output:
4
Constraint:
~1<n\le10000~; ~0\le Ai \le 32000~;</p>
Relax max
Nộp bàiPoint: 8
Cho dãy gồm N ~(1 \le N \le 10^5)~ số nguyên ~A_1, A_2, A_N; (0 < A_i \le 10^5)~. Với bộ ba số (i,j,k) trong đó ~1 \le i < j < k \le N~ hãy tìm giá trị ~S= 3A_i - A_j - A_k~ sao cho S đạt giá trị lớn nhất.
Input:
Được cho bởi tệp relaxmax.inp có cấu trúc như sau:
- Dòng đầu tiên chứa số nguyên N.
- Dòng thứ hai chứa N số nguyên ~A_1, A_2,..., A_N~ giữa các số cách nhau một khoảng trắng.
Output:
Được cho bởi tệp relaxmax.out có cấu trúc như sau:
- In ra một số duy nhất là số S lớn nhất tìm được.
Example
Input
9
95 5 74 65 89 62 3 2 37
Output
280
Up max
Nộp bàiPoint: 8
Cho dãy gồm N ~(1 \le N \le 10^5)~ số nguyên ~A_1, A_2, A_N; (0 < A_i \le 10^5)~. Với bộ ba số (i,j,k) trong đó ~1 \le i < j < k \le N~ hãy tìm giá trị ~S= A_i - A_j + A_k~ sao cho S đạt giá trị lớn nhất.
Input:
Được cho bởi tệp upmax.inp có cấu trúc như sau:
- Dòng đầu tiên chứa số nguyên N.
- Dòng thứ hai chứa N số nguyên ~A_1, A_2,..., A_N~ giữa các số cách nhau một khoảng trắng.
Output:
Được cho bởi tệp upmax.out có cấu trúc như sau:
- In ra một số duy nhất là số S lớn nhất tìm được.
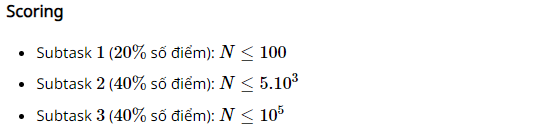
Example
Input
5
2 3 5 7 -3
Output
6
Lower max
Nộp bàiPoint: 8
Cho dãy gồm N ~(1 \le N \le 10^5)~ số nguyên ~A_1, A_2, A_N; (0 < A_i \le 10^5)~. Với bộ ba số (i,j,k) trong đó ~1 \le i < j < k \le N~ hãy tìm giá trị ~S= 2A_i + A_j + 3A_k~ sao cho S đạt giá trị nhỏ nhất.
Input:
Được cho bởi tệp lowmax.inp có cấu trúc như sau:
- Dòng đầu tiên chứa số nguyên N.
- Dòng thứ hai chứa N số nguyên ~A_1, A_2,..., A_N~ giữa các số cách nhau một khoảng trắng.
Output:
Được cho bởi tệp lowmax.out có cấu trúc như sau:
- In ra một số duy nhất là số S nhỏ nhất tìm được.
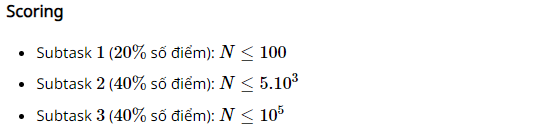
Example
Input
9
5 4 4 4 1 4 6 8 7
Output
15
Three max
Nộp bàiPoint: 8
Cho dãy gồm N ~(1 \le N \le 10^5)~ số nguyên ~A_1, A_2, A_N; (0 < A_i \le 10^5)~. Với bộ ba số (i,j,k) trong đó ~1 \le i < j < k \le N~ hãy tìm giá trị ~S= 3A_i + 2A_j - 5A_k~ sao cho S đạt giá trị lớn nhất.
Input:
Được cho bởi tệp three.inp có cấu trúc như sau:
- Dòng đầu tiên chứa số nguyên N.
- Dòng thứ hai chứa N số nguyên ~A_1, A_2,..., A_N~ giữa các số cách nhau một khoảng trắng.
Output:
Được cho bởi tệp three.out có cấu trúc như sau:
- In ra một số duy nhất là số S lớn nhất tìm được.
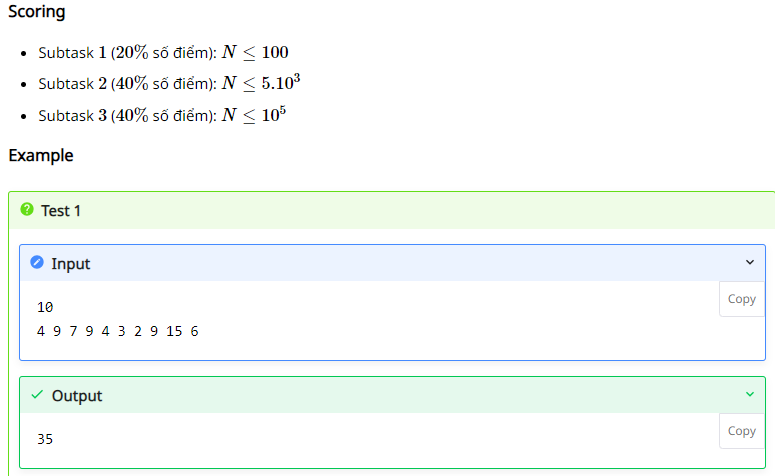
Giá trị lớn nhất
Nộp bàiPoint: 8
Cho dãy số nguyên dương A gồm N phần tử ~A_i~ (~1 \le i \le N~; ~3 \le N \le 10^6~; ~1 \le A_i \le 2.10^9~) và biểu thức ~M = A_i – 3A_j + 2A_k~ với ~A_i~, ~A_j~, ~A_k~ thuộc dãy số A (~1 \le i < j < k < N~).
Yêu cầu: Tìm giá trị M lớn nhất.
Input:
- Dòng 1: Ghi số nguyên dương N.
- Dòng 2: Ghi N số nguyên dương ~Ai~, mỗi số cách nhau một khoảng trống.
Output:
- Dòng 1: Ghi ra số M tìm được.
Example:
Input:
5
8 1 2 6 3
Output:
17
Constraints:
- Có 70% số lượng bộ test tương ứng với ~3 < N \le 300~; ~1 \le A_i \le 65535~
- Có 30% số lượng bộ test tương ứng với ~300 < N \le 10^6~; ~1 \le A_i \le 2.10^9~