Chữ số tận cùng của một số là chữ số cuối cùng của số đó. Ví dụ: số 123 có chữ số tận cùng là 3; số 5 có chữ số tận cùng là 5.

Yêu cầu: Cho hai số nguyên dương ~A~,~N~, hãy tìm chữ số tận cùng của ~A^N~.

Dữ liệu vào:

• Một dòng duy nhất ghi hai số nguyên dương lần lượt là ~A~ và ~N~. Các số viết cách nhau một dấu cách.

Kết quả:

• Gồm một số nguyên duy nhất là chữ số tận cùng tìm được.

Ví dụ:

Input1

2 10

Output1

4

• Giải thích: 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2=1024

Input2

12 3

Output2

8

• Giải thích: 12 x 12 x 12=1728

Ràng buộc:

• Có 60% số điểm tương ứng với: ~1≤A,N≤9~;
• Có 20% số điểm tương ứng với: ~1≤A,N≤15~;
• Có 20% số điểm tương ứng với: ~1≤A,N≤10^8~.

Trọng số của một xâu ~S~ là trung bình cộng các chữ số trong xâu S đó. Nếu xâu S không có chữ số nào thì có trọng số là 0. Ví dụ: Xâu ab011c2 có trọng số là 1.

Yêu cầu: Cho ~N~ xâu ký tự, hãy tìm xâu có trọng số lớn nhất. Nếu có nhiều xâu có trọng số bằng nhau thì ghi ra xâu đầu tiên tìm được, nếu không tìm thấy xâu có trọng số lớn nhất thì ghi 0.

Dữ liệu vào:

• Dòng đầu ghi số nguyên N là số lượng xâu (1≤N≤100);
• N dòng tiếp theo, mỗi dòng ghi một xâu S.

Kết quả:

• Ghi ra kết quả tìm được.

Ví dụ:

Input

3
aaaaaaa
10a3bb2021
100256

Output

100256

• Giải thích: 1+0+0+2+5+6=14/6= 2.33 lớn nhất

Ràng buộc:

• 60% số test tương ứng với xâu S có độ dài không quá 255;
• 40% số test tương ứng với xâu S có độ dài không quá 1000.

Một số nguyên dương ~X~ được gọi là số đặc biệt nếu thỏa mãn hai điều kiện sau:

• ~X~ là số nguyên tố;

• Số lượng chữ số chẵn và số lượng chữ số lẻ trong ~X~ là khác nhau.

Yêu cầu: Cho một dãy số nguyên gồm ~N~ phần tử ~A_1,A_2,…,A_N~. Hãy đếm số lượng phần tử là số đặc biệt của dãy ~A~.

Dữ liệu vào:

• Dòng thứ nhất ghi số nguyên dương ~N~;
• Dòng thứ hai chứa N số nguyên ~A_1,A_2,…,A_N~. Các số viết cách nhau một dấu cách.

Kết quả:

• Gồm một số nguyên duy nhất là số lượng số đặc biệt đếm được.

Ví dụ:

Input

5
121 311 122 23 241

Output

2

Giải thích: Dãy ~A~ có hai số đặc biệt là: 311 và 241

Ràng buộc:

• Có 60% số điểm tương ứng với: ~1≤N≤300~; ~1≤A_i≤50000~;
• Có 20% số điểm tương ứng với: ~1≤N≤300~; ~|A_i |≤10^{12}~;
• Có 20% số điểm tương ứng với: ~1≤N≤2*10^6~; ~|A_i| ≤ 2*10^6~.

An thích học về bảng số. Bạn ấy tạo ra bảng số ~A~ có kích thước ~M*N~ theo quy luật như sau:

- Bảng có M dòng đánh số từ 1 đến M;

- Bảng có N cột đánh số từ 1 đến N;

Tại vị trí dòng i và cột j trên bảng số sẽ được ghi số ~(i-1)*N+j~ nếu (~i+j~) là số chẵn, và ghi số 0 nếu (~i+j~) là số lẻ (~1≤i≤M~,~1≤j≤N~).

Yêu cầu: Cho hai số nguyên dương ~M~,~N~. Hãy tính tổng tất cả các số được ghi trên bảng.

Dữ liệu vào:

• Chỉ có một dòng duy nhất ghi hai số nguyên lần lượt là ~M~ và ~N~. Các số viết cách nhau một dấu cách.

Kết quả:

• Ghi ra một số nguyên duy nhất là tổng các số được ghi trên bảng số. Vì số này có thể rất lớn nên chỉ in ra đáp án sau khi chia lấy dư cho 1532023.

Ví dụ:

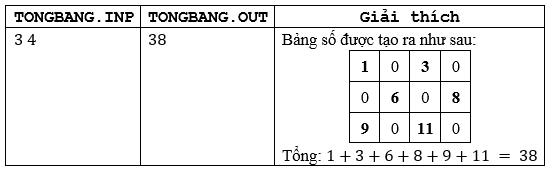
• Giải thích: Dãy ~A~ có hai số đặc biệt là: 311 và 241

Ràng buộc:

• Có 60% số điểm tương ứng với: ~1 ≤ M,N ≤ 500~;
• Có 20% số điểm tương ứng với: ~1 ≤ M,N ≤ 10^5~;
• Có 20% số điểm tương ứng với: ~1 ≤ M,N ≤ 10^9~.