Yêu cầu:

Cho 1 dãy số nguyên gồm ~n~ số cho trước. Hãy đếm tất cả các số chính phương, nguyên tố, hoàn hảo, phong phú trong đoạn từ vị trí ~x~ đến vị trí ~y~ trong dãy.

Giải thích:

• Ước thực sự của 1 số là tập hợp tất cả các ước dương nhỏ hơn nó.
• Số chính phương là số có căn bậc 2 của nó là một số nguyên.
• Số nguyên tố là số chỉ có 2 ước là 1 và chính nó.
• Số hoàn hảo là số có tổng các ước thực sự của nó bằng chính nó. Ví dụ, số 6 có tổng các ước số (không kể 6) là 1 + 2 + 3 = 6. Do đó 6 là một số hoàn hảo.
• Số phong phú là số có tổng các ước thực sự của số đó lớn hơn số đó. Ví dụ, số 12 có tổng các ước số (không kể 12) là 1 + 2 + 3 + 4 + 6 = 16 > 12. Do đó 12 là một số phong phú.

Input:

• Dòng 1: Ghi số nguyên ~𝑛~, (~1 \le n \le 10^5~).
• Dòng 2: Ghi ~𝑛~ số nguyên ~A_1, A_2,...,A_n, 1 \le A_i \le 10^6~
• Dòng 3: Ghi số nguyên dương ~q~ - số bộ test.
• ~q~ dòng tiếp theo, mỗi dòng ghi 2 số nguyên dương ~x~, ~y~ (~1 \le x \le y \le n~; ~1 \le q \le 10^5~)

Output:

• Gồm q dòng: Ứng với mỗi cặp số x,y in ra 4 số nguyên dương lần lượt là số lượng các số chính phương, nguyên tố, hoàn hảo, phong phú tìm được trong đoạn từ ~x~ đến ~y~.

Example:

Input:

7
2 3 5 7 12 8 6
2
1 3
2 4

Output:

0 3 0 0
0 3 0 0

P/S:

• Dữ liệu vào được nhập từ bàn phím

An thích học vẽ bảng số. Bạn ấy tạo ra bảng số A có kích thước ~M×N~ theo quy luật như sau:

• Bảng có ~M~ dòng đánh số từ 1 đến ~M~;

• Bảng có ~N~ cột đánh số từ 1 đến ~N~;

Tại vị trí dòng i và cột j trên bảng số sẽ được ghi số ~(i-1)*N + j~ nếu ~i+j~ là số chẵn, và ghi số 0 nếu i+j là số lẻ (~1 \le i \le M~, ~1 \le j \le N~)

Yêu cầu: Cho hai số nguyên dương ~𝑀~,~𝑁~. Hãy tính tổng tất cả các số được ghi trên bảng.

Dữ liệu vào:

• Gồm một dòng duy nhất ghi hai số nguyên dương lần lượt là ~M~ và ~N~. Các số viết cách nhau một dấu cách.

Kết quả:

• Một số nguyên duy nhất là tổng các số được ghi trên các dòng lẻ của bảng số.

Ví dụ:

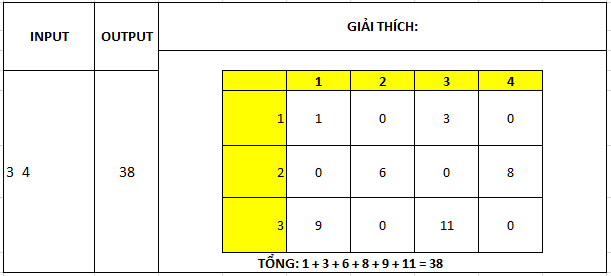
Ràng buộc

• Sub 1: Có 20% số điểm ứng với ~1 \le M,N \le 10^3~;
• Sub 2: Có 40% số điểm ứng với ~1 \le M,N \le 10^6~;
• Sub 3: Có 40% số điểm ứng với ~10^6 < M,N \le 10^7~. Vì kết quả ở Sub 3 có thể rất lớn nên chỉ in ra đáp án sau khi chia lấy dư cho ~10^9 + 7~.; Chỉ có kết quả ở trường hợp này mới chia lấy dư cho ~10^9 + 7~.