CONTEST 55: LUYỆN ĐỀ TS CÁC TỈNH
21A. Phú Yên - Bài 1 - Tìm mã OTP (2 điểm)
Nộp bàiPoint: 10
Tuấn là người rất đam mê lập trình điều khiển Robot. Tuấn đã lập trình cho các Robot của mình với nhiều tính năng hấp dẫn. Để điều khiển được Robot, đầu tiên Robot yêu cầu cung cấp đúng chuỗi mật khẩu ban đầu, nếu đúng Robot hỏi lần thứ hai bằng một yêu cầu xác nhận mã OTP, mã OTP là số lượng ký tự khác nhau của mật khẩu ban đầu. Nam được Tuấn cho mượn các Robot để khám phá, nhưng Tuấn chỉ cung cấp mật khẩu ban đầu, còn mã OTP Nam phải suy luận để tìm. Biết rằng khi lập mật khẩu Tuấn chỉ sử dụng các chữ cái tiếng Anh (chữ in thường, in hoa) và các chữ số từ 0 đến 9.
Yêu cầu: Bạn hãy giúp Nam tìm mã OTP tương ứng với mật khẩu ban đầu.
Input
- Gồm nhiều dòng, dòng thứ i là xâu ký tự tương ứng là mật khẩu ban đầu của Robot thứ i (~0 < i ≤ 10^3~), độ dài xâu ký tự không quá 255.
Output
- Gồm nhiều dòng, mỗi dòng ghi số ~N~, là mã OTP tương ứng với mật khẩu ban đầu của robot thứ i
Examples
Input
ToithichlaptrinhTINHOC
Output
16
Input
Abcd1234Bacsd12
Output
11
27C. Tiền Giang - Bài 3 - Vòng tròn (2 điểm)
Nộp bàiPoint: 10
Bo đang chơi một game. Ban đầu, Bo có một vòng tròn bán kính ~k~. Trên màn hình game còn có ~n~ vòng tròn khác, vòng tròn thứ ~i~ có bán kính là ~A_i~. Bo có thề điều khiền vòng tròn của mình để chạm vào các vòng tròn khác. Mỗi khi vòng tròn của Bo chạm vào một vòng tròn khác thì một trong hai khả năng có thể xảy ra:
Nếu bán kính vòng tròn do Bo điều khiển lớn hơn hay bằng bán kính vòng tròn bị chạm vào thì vòng tròn bị chạm sẽ tan vỡ, còn vòng tròn của Bo trở nên lớn hơn và bán kính của nó sẽ bằng tổng bán kính vòng tròn hiện tại của Bo với bán kính vòng tròn bị chạm đó. Nếu bán kính vòng tròn do Bo điều khiến nhỏ hơn bán kính vòng tròn bị chạm vào thì kết thúc game. Bo chơi game rất giỏi. Bạn ấy luôn tìm cách chơi sao cho khi kết thúc game thì bán kính vòng tròn của bạn ấy là lớn nhất.
Yêu cầu: Tìm bán kính lớn nhất có thể đạt được của vòng tròn.
Input
Dòng thứ nhất: gồm hai số nguyên dương lần lượt là ~n~ và ~k~. Trong đó, ~n~ là số lượng vòng tròn, ~k~ là bán kính vòng tròn của Bo, giữa ~n~ và ~k~ được cách nhau bởi một dấu cách. (~1 ≤ n ≤ 10^3~, ~1 ≤ k ≤ 10^6~)
Dòng thứ hai: gồm ~n~ số nguyên dương ~A_i~ lần lượt là bán kính của ~n~ vòng tròn. (~1 ≤ A_i ≤ 10^6~)
Output
- Gồm một số nguyên dương là bán kính lớn nhất cần tìm.
Example
Input
5 4
7 68 3 2 20
Output
16
Note
Ban dầu, có 5 vòng tròn (~n = 5~) với bán kính lần lượt là 7, 68, 3, 2, 20 và vòng tròn của Bo có bán kính là ~k~ = 4.
Lần 1: Vòng tròn của Bo chạm vòng tròn có bán kính là 2 → vòng tròn của Bo có bán kính mới là 4 + 2 = 6.
Lần 2: Vòng tròn của Bo chạm vòng tròn có bán kính là 3 → vòng tròn của Bo có bán kính mới là 6 + 3 = 9.
Lần 3: Vòng tròn của Bo chạm vòng tròn có bán kính là 7 → vòng tròn của Bo có bán kính mới là 9 + 7 = 16.
Đến đây, còn hai vòng tròn có bán kính là 20 và 68. Hai bán kính này đều lớn hơn bán kính vòng của Bo nên kết thúc game.
Vậy bán kính lớn nhất cần tìm là 16.
28D. Vĩnh Long - Bài 4 - Bút màu (2 điểm)
Nộp bàiPoint: 10
Bài khó trong đề thi TS10C năm nay là một bài về mảng. Sinh có ~N~ cây bút màu, mỗi màu được ký hiệu là số nguyên dương ~a_i~, có thể có những cây bút cùng màu. Sinh cần xếp chúng vào đầy các hộp để bảo quản, mỗi hộp được chứa đúng ~K~ bút cùng màu (số lượng hộp bút để chứa bút luôn đảm bảo). Những cây bút màu không được xếp vào hộp, Sinh sẽ tặng trẻ em có hoàn cảnh khó khăn để các em tập vẽ trong hè chuẩn bị cho năm học sau.
Yêu cầu: Hỏi Sinh có bao nhiêu màu bút khác nhau và Sinh sẽ tặng trẻ em có hoàn cảnh khó khăn bao nhiêu cây bút màu?
Input
Dòng đầu tiên là hai số nguyên dương ~N~ (~1 ≤ N ≤ 10^4~) và ~K~ (~K < N~) cách nhau ít nhất một dấu cách, là số lượng cây bút màu và số lượng bút chứa được trong hộp.
~N~ dòng tiếp theo là ~N~ số, số thứ ~i~ là số nguyên dương ~a_i~ (~a_i ≤ 10^6~) - là màu của cây bút thứ ~i~. Mỗi số trên 1 dòng.
Output
Dòng đầu tiên in một số nguyên duy nhất, là số màu khác nhau trong ~N~ cây bút.
Dòng thứ hai in một số nguyên duy nhất là số lượng cây bút màu sẽ tặng.
Examples
Input
7 2
1
2
6
1
4
3
3
Output
5
3
Input
7 4
5
2
3
5
5
3
5
Output
3
3
Input
6 2
1
1
7
7
4
4
Output
3
0
Note
- Ở ví dụ một, 7 cây bút có 5 màu khác nhau (1, 2, 3, 4, 6). Xếp hai cây bút có màu 1 vào hộp và hai cây bút màu 3 vào hộp khác, thì còn 3 cây bút có màu 2, 4, 6 để tặng (do hộp chứa 2 cây bút cùng loại nhưng mỗi loại này chỉ có một cây).
Ở ví dụ hai, 7 cây bút có 3 màu (2, 3, 5). Sau khi xếp 3 cây bút có màu 5 vào hộp thì còn 4 cây bút để tặng: 1 cây màu 2, 2 cây màu 3, 1 cây màu 5.
Ở ví dụ ba, 6 cây bút có 3 màu (1, 4, 7). Xếp 2 cây bút có màu 1 vào hộp, 2 cây bút màu 4 vào hộp khác, 2 cây bút màu 7 vào hộp khác nữa thì không còn cây bút màu nào để tặng.
27E. Tiền Giang - Bài 5 - Cắt hình (2 điểm)
Nộp bàiPoint: 10
Bé Bo có một mảnh giấy hình chữ nhật gồm ~m~ x ~n~ ô vuông bằng nhau, với ~m~ là chiều dài và ~n~ là chiều rộng mảnh giấy. Bo tìm cách cắt từ mành giấy này đề mỗi lần cắt được hình vuông có diện tích lớn nhất. Thao tác này được thực hiện nhiều lần như thế đối với phần giấy còn thừa lại cho đến khi hết giấy thừa.
Yêu cầu: Đếm số hình vuông Bo có thể cắt được
Input
- Gồm một dòng chứa hai số nguyên dương lần lượt là ~m~ và ~n~, giữa ~m~ và ~n~ được cách nhau bởi một dấu cách. (~1 ≤ n ≤ m ≤ 10^9~)
Output
- Một số nguyên dương là số hình vuông Bo cắt được.
Examples
Input
8 3
Output
5
Input
21 4
Output
9
Note
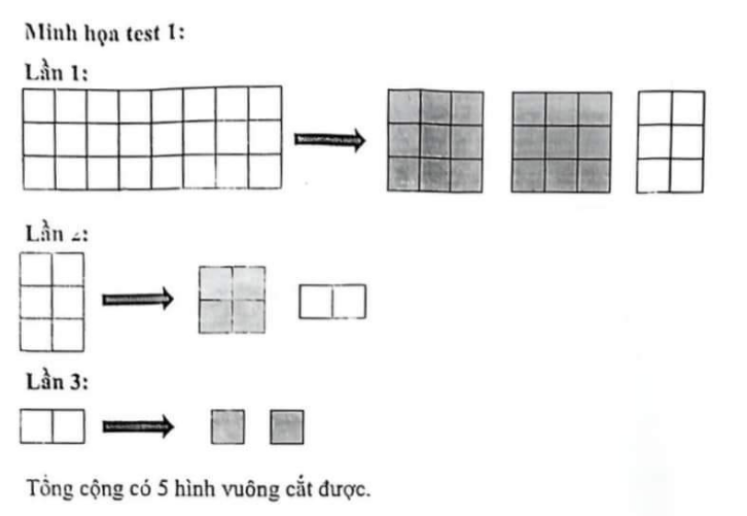
HSG 12 QB 2024 - 2025 (Câu 2)
Nộp bàiPoint: 10
Nhà hàng 𝐴𝐵𝐶 là nhà hàng nổi tiếng ở tỉnh Quảng Bình, trong đó có hai món ăn được yêu thích nhất là bánh bèo và bánh lọc. Năm nay, nhà hàng 𝐴𝐵𝐶 tổ chức một cuộc thi giữa ~𝑁~ đầu bếp trên cả nước. Trong cuộc thi này, mỗi đầu bếp sẽ chế biến một dĩa bánh bèo và một dĩa bánh lọc. Vì mỗi đầu bếp có một thế mạnh khác nhau nên mỗi dĩa bánh có độ ngon khác nhau, dĩa bánh bèo thứ ~𝑖~ có độ ngon là 𝑎 và dĩa bánh lọc thứ ~𝑖~ có độ ngon là ~𝑏~. Khách hàng sẽ được thưởng thức miễn phí các món bánh do ~𝑁~ đầu bếp chế biến. Một nhóm khách hàng được phép chọn ~𝑁~ dĩa bánh, trong đó không có hai dĩa bánh nào do cùng một đầu bếp chế biến.
Yêu cầu: Với mỗi số nguyên dương ~𝑘~ (~1 ≤ 𝑘 ≤ 𝑁~), hãy tính tổng độ ngon lớn nhất có thể khi nhóm khách hàng chọn ~𝑘~ dĩa bánh bèo và ~𝑁-𝑘~ dĩa bánh lọc.
Dữ liệu vào:
- Dòng 1: Ghi số nguyên dương ~𝑁~ (~1 ≤ 𝑁 ≤ 10^5~) là số dĩa bánh bèo, đồng thời cũng là số dĩa bánh lọc.
- Dòng 2: Ghi dãy ~𝑎~ gồm 𝑁 số nguyên dương ~𝑎_1 ,𝑎_2 ,…,𝑎_N~ (~1 ≤ 𝑎_i≤ 10^9 ;1 ≤ 𝑖 ≤ 𝑁~) lần lượt là độ ngon của ~𝑁~ dĩa bánh bèo, các số được ghi cách nhau một dấu cách.
- Dòng 3: Ghi dãy ~𝑏~ gồm ~𝑁~ số nguyên dương ~𝑏_1 ,𝑏_2 ,…,𝑏_N~ (~1 ≤ 𝑏_i ≤ 10^9 ;1 ≤ 𝑖 ≤ 𝑁~) lần lượt là độ ngon của ~𝑁~ dĩa bánh lọc, các số được ghi cách nhau một dấu cách.
Dữ liệu ra:
- Dòng 1: Ghi 𝑁 số nguyên dương ~𝑡_1 ,𝑡_2 ,…,𝑡_N~ , trong đó ~𝑡~ (~1 ≤ 𝑘 ≤ 𝑁~) là tổng độ ngon lớn nhất tìm được khi chọn ~𝑘~ dĩa bánh bèo và ~𝑁 - 𝑘~ dĩa bánh lọc, các số được ghi cách nhau một dấu cách.
Ví dụ:
Input
6
1 4 5 7 9 12
13 12 9 6 2 1
Output
54 61 62 58 50 38
Ràng buộc:
- Có 40% số test tương ứng với 40% số điểm: Dãy ~𝑎~ được sắp xếp không giảm, dãy ~𝑏~ được sắp xếp không tăng và ~1 ≤ 𝑁 ≤ 10^3~ ;
- Có 20% số test tương ứng với 40% số điểm: Dãy ~𝑎~ được sắp xếp không giảm, dãy 𝑏 được sắp xếp không tăng và ~10^3 < 𝑁 ≤ 10^5~ ;
- Có 20% số test tương ứng với 20% số điểm: ~𝑁 ≤ 20~;
- Có 20% số test tương ứng với 20% số điểm: Không có ràng buộc gì thêm.
Hai tập hợp
Nộp bàiPoint: 20
Hãy đếm số cách mà các số ~1,2,…,n~ có thể được chia thành hai tập hợp có tổng bằng nhau.
Ví dụ, với ~n=7~, có 4 cách chia:
- {1,3,4,6} và {2,5,7}
- {1,2,5,6} và {3,4,7}
- {1,2,4,7} và {3,5,6}
- {1,6,7} và {2,3,4,5}
Input
Gồm một dòng duy nhất chứa số nguyên n.
Output
In đáp án - số cách thoả mãn chia lấy dư cho ~10^9 +7~.
Constraints
~1≤n≤500~
Example
Sample input
7
Sample output
4