Tính tổng và số lượng các số hạng của dãy số sau: S= 3 + 6 + 9 + 12 +…..+ N

Input:

• Nhập vào một số nguyên dương N (N chia hết cho 3)

Output:

• Ghi ra số nguyên S là tổng các số hạng của dãy số trên.

Example:

Input:

12

Output:

30

Constraints:

~0 < N \le 10^9~

Số nguyên ~K~ được gọi là ước của ~N~ khi ~N~ chia hết cho K. Ví dụ: ~N=6~, ~N~ có 4 ước nguyên dương là: 1,2,3,6.

Cho số nguyên dương ~N~ và dãy gồm ~N~ số nguyên ~A_1, A_2, A_3,…, A_N~.

Yêu cầu: Hãy tìm và in ra số có nhiều ước nguyên dương nhất. Nếu có nhiều số cùng có số lượng ước lớn nhất và bằng nhau thì in ra số đầu tiên tìm thấy trong dãy đã cho.

Input:

• Dòng 1. Ghi số nguyên dương ~N~
• Dòng 2. Ghi ~N~ số nguyên ~A_1, A_2, A_3,…, A_N~.

Output:

• In ra số nguyên có nhiều ước nguyên dương nhất trong dãy đã cho.

Example:

Input:

5
1 2 12 16 17

Output:

12
Giải thích: trong 5 số đã cho, số 12 có 6 ước và nhiều nhất.

Constraints:

~1 < N,A_i \le 10^6~

Bạn đang biên đạo một chương trình xiếc với nhiều động vật khác nhau. Đối với một hành động, bạn được cung cấp hai con chuột túi trên một đường thẳng và cùng nhảy về một hướng.

• Con chuột túi đầu tiên bắt đầu tại vị trí ~x_1~ và di chuyển với tốc độ ~v_1~ mét trên mỗi lần nhảy.

• Con chuột túi thứ hai bắt đầu tại vị trí ~x_2~ và di chuyển với tốc độ ~v_2~ mét trên mỗi lần nhảy.

  

Bạn đang thắc mắc liệu với cùng số lần nhảy hai con chuột túi này có gặp nhau tại một điểm trong quá trình nhảy hay không.

Input:

• Nhập vào 4 số nguyên theo thứ tự ~x_1, v_1, x_2, v_2~

Output:

• Nếu 2 chú chuột có thể gặp nhau tại một điểm với cùng số lần nhảy thì ghi YES, nếu không thì ghi NO.

Example:

Input:

0 3 4 2

Output:

YES

Hai con kanguru nhảy qua chuỗi địa điểm sau:

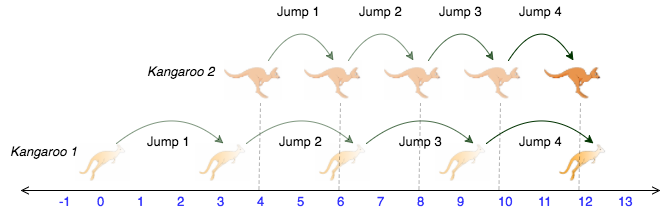
Constraints:

~0 \le x_1 \le x_2 \le 10000~ ; ~0 \le v_1, v_2 \le 10000~

Có N cây gỗ, có chiều cao lần lượt là ~A_1,A_2,...,A_N~. Bạn cần lấy một lượng gỗ độ cao tối thiểu là M bằng cách chặt từ N cây theo cách như sau: chặt tất cả những phần thừa của các cây có độ cao lớn hơn H.

Yêu cầu: Hãy tìm giá trị H lớn nhất để bạn có thể lấy được lượng gỗ tối thiểu là M.

Input:

• Dòng 1 chứa 2 số nguyên N và M .
• Dòng 2 chứa N số nguyên ~A_1,A_2,...,A_N~, là chiều cao mỗi cây gỗ tương ứng. Giả sử luôn tồn tại cách chặt.

Output:

• Số H duy nhất là kết quả bài toán trên.

Example:

Input:

4 7
20 15 10 17

Output:

15
Giải thích:  
Cây 1 chặt được (20-15)=5.
Cây 4 chặt được (17-15)=2.
Tổng số gỗ chặt được nếu H=15 là 7.

Constraints:

~1 \le N \le 2.10^5 ; 1 <= M <= 2.10^6 ; A_i \le 10^5~